GFM: alternate maximization and information criterion

Wei Liu

2023-08-10

Source: vignettes/GFM.Simu.Rmd

In this tutorial, we show that the alternate maximization (AM) is used in the first step of the two-step estimation method and the information criterion (IC) method is adopted to choose the number of factors.

Fit GFM model using simulated data

The package can be loaded with the command:

library("GFM")
#> Loading required package: doSNOW
#> Loading required package: foreach
#> Loading required package: iterators
#> Loading required package: snow
#> Loading required package: parallel
#> 
#> Attaching package: 'parallel'
#> The following objects are masked from 'package:snow':
#> 
#>     clusterApply, clusterApplyLB, clusterCall, clusterEvalQ,
#>     clusterExport, clusterMap, clusterSplit, makeCluster, parApply,
#>     parCapply, parLapply, parRapply, parSapply, splitIndices,
#>     stopCluster
#> GFM :  Generalized factor model is implemented for ultra-high dimensional data with mixed-type variables.
#> Two algorithms, variational EM and alternate maximization, are designed to implement the generalized factor model,
#> respectively. The factor matrix and loading matrix together with the number of factors can be well estimated.
#> This model can be employed in social and behavioral sciences, economy and finance, and  genomics,
#> to extract interpretable nonlinear factors. More details can be referred to
#> Wei Liu, Huazhen Lin, Shurong Zheng and Jin Liu. (2021) <doi:10.1080/01621459.2021.1999818>.   Check out our Package website (https://feiyoung.github.io/GFM/docs/index.html) for a more complete description of the methods and analyses
set.seed(1) # set a random seed for reproducibility.

GFM can handle data with homogeneous normal variables

First, we generate the data with homogeneous normal variables.

## Homogeneous  normal variables
  dat <- gendata(q = 2, n=100, p=100, rho=3)

Then, we set the algorithm parameters and fit model

# Obtain the observed data
  XList <- dat$XList # this is the data in the form of matrix list.
  str(XList)
#> List of 1
#>  $ : num [1:100, 1:100] -1.031 1.528 -0.565 1.288 -0.667 ...
#>   ..- attr(*, "dimnames")=List of 2
#>   .. ..$ : NULL
#>   .. ..$ : NULL
  X <- dat$X # this is the data in form of matrix
# set variables' type, 'gaussian' means there is  continous variable type.
  types <- 'gaussian'

Third, we fit the GFM model with user-specified number of factors.

# specify q=2
  gfm1 <- gfm(XList, types, algorithm="AM", q=2, verbose = FALSE)
  
  # measure the performance of GFM estimators in terms of canonical correlations
  measurefun(gfm1$hH, dat$H0, type='ccor')
#> [1] 0.9893027
  measurefun(gfm1$hB, dat$B0, type='ccor')
#> [1] 0.9931255

The number of factors can also be determined by data-driven manners.

GFM outperforms LFM in analyzing data with heterogeous normal variables

First, we generate the data with heterogeous normal variables and set the parameters of algorithm.

  dat <- gendata(seed=1, n=100, p=100, type='heternorm', q=2, rho=1)
 # Obtain the observed data
  XList <- dat$XList # this is the data in the form of matrix list.
  str(XList)
#> List of 1
#>  $ : num [1:100, 1:100] 0.7458 -2.006 1.705 0.0484 3.094 ...
#>   ..- attr(*, "dimnames")=List of 2
#>   .. ..$ : NULL
#>   .. ..$ : NULL
  X <- dat$X # this is the data in form of matrix
# set variables' type, 'gaussian' means there is  continous variable type.
  types <- 'gaussian'

Third, we fit the GFM model with user-specified number of factors and compare the results with that of linear factor models.

# specify q=2
  gfm1 <- gfm(XList, types,  algorithm="AM", q=2, verbose = FALSE)
  
  # measure the performance of GFM estimators in terms of canonical correlations
  corH_gfm <- measurefun(gfm1$hH, dat$H0, type='ccor')
  corB_gfm <- measurefun(gfm1$hB, dat$B0, type='ccor')
  
  lfm1 <- Factorm(X, q=2)
  corH_lfm <- measurefun(lfm1$hH, dat$H0, type='ccor')
  corB_lfm <- measurefun(lfm1$hB, dat$B0, type='ccor')
  
  library(ggplot2)
#> Warning: package 'ggplot2' was built under R version 4.1.3
  df1 <- data.frame(CCor= c(corH_gfm, corH_lfm, corB_gfm, corB_lfm),
                    Method =factor(rep(c('GFM', "LFM"), times=2)),
                    Quantity= factor(c(rep('factors',2), rep("loadings", 2))))
  ggplot(data=df1, aes(x=Quantity, y=CCor, fill=Method)) + geom_bar(position = "dodge", stat="identity",width = 0.5)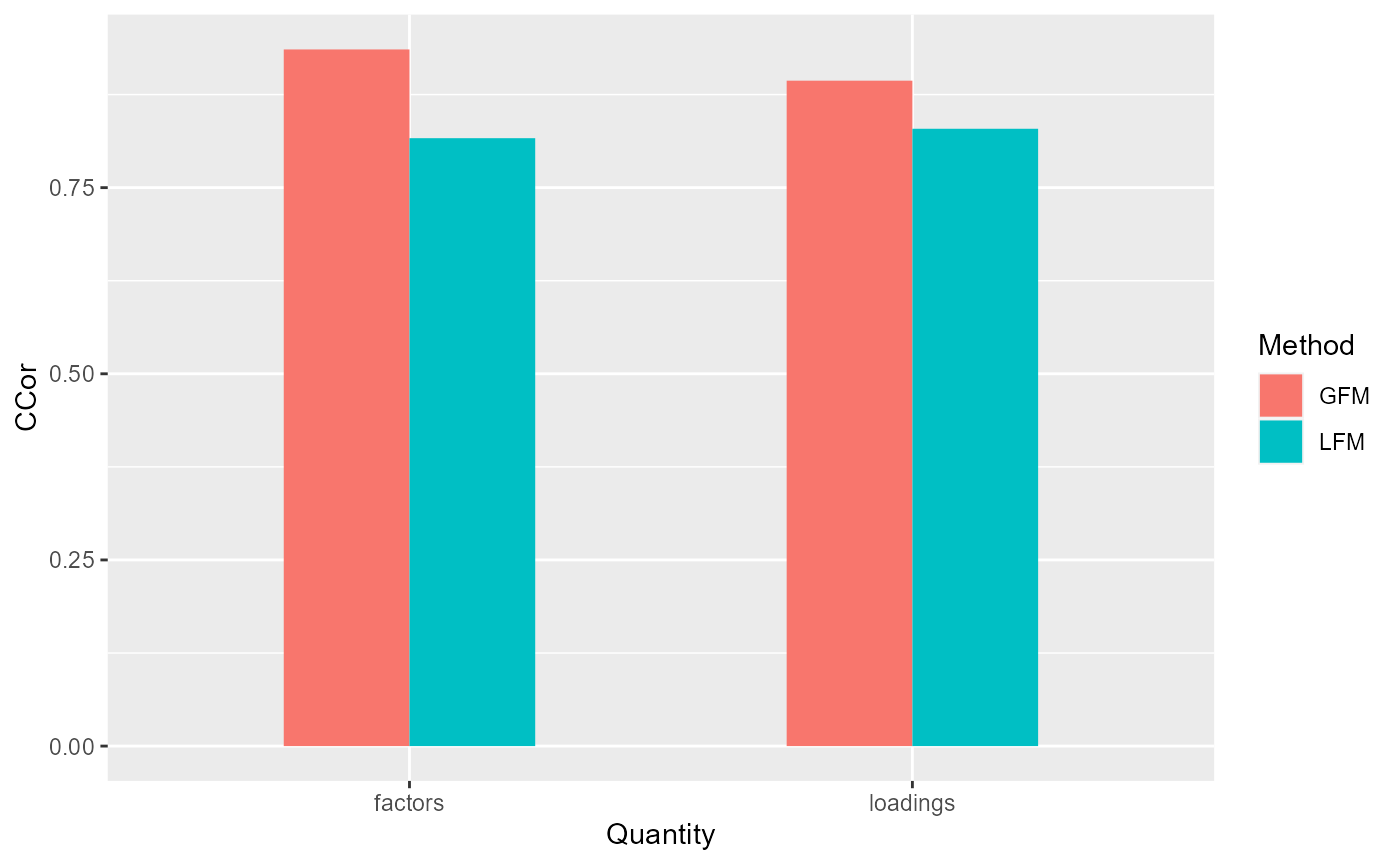

The number of factors can also be determined by data-driven manners.

GFM outperforms LFM in analyzing data with Count(Poisson) variables

First, we generate the data with Count(Poisson) variables and set the parameters of algorithm.

  q <- 3; p <- 200
  dat <- gendata(seed=1, n=200, p=p, type='pois', q=q, rho=4)
  # Obtain the observed data
  XList <- dat$XList # this is the data in the form of matrix list.
  str(XList)
#> List of 1
#>  $ : int [1:200, 1:200] 0 3 4 1 0 4 2 3 1 1 ...
  X <- dat$X # this is the data in form of matrix
# set variables' type, 'gaussian' means there is  continous variable type.
  types <- 'poisson'

Second, we we fit the GFM models given the true number of factors.

  system.time(
   gfm1 <- gfm(XList, types,  algorithm="AM", q=3, verbose = FALSE)
  )
#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred
#>    user  system elapsed 
#>    4.36    0.03    9.40

Third, we compare the results with that of linear factor models.


  # measure the performance of GFM estimators in terms of canonical correlations
  corH_gfm <- measurefun(gfm1$hH, dat$H0, type='ccor')
  corB_gfm <- measurefun(gfm1$hB, dat$B0, type='ccor')
  
  lfm1 <- Factorm(X, q=3)
  corH_lfm <- measurefun(lfm1$hH, dat$H0, type='ccor')
  corB_lfm <- measurefun(lfm1$hB, dat$B0, type='ccor')
  
  library(ggplot2)
  df1 <- data.frame(CCor= c(corH_gfm, corH_lfm, corB_gfm, corB_lfm),
                    Method =factor(rep(c('GFM', "LFM"), times=2)),
                    Quantity= factor(c(rep('factors',2), rep("loadings", 2))))
  ggplot(data=df1, aes(x=Quantity, y=CCor, fill=Method)) + geom_bar(position = "dodge", stat="identity",width = 0.5)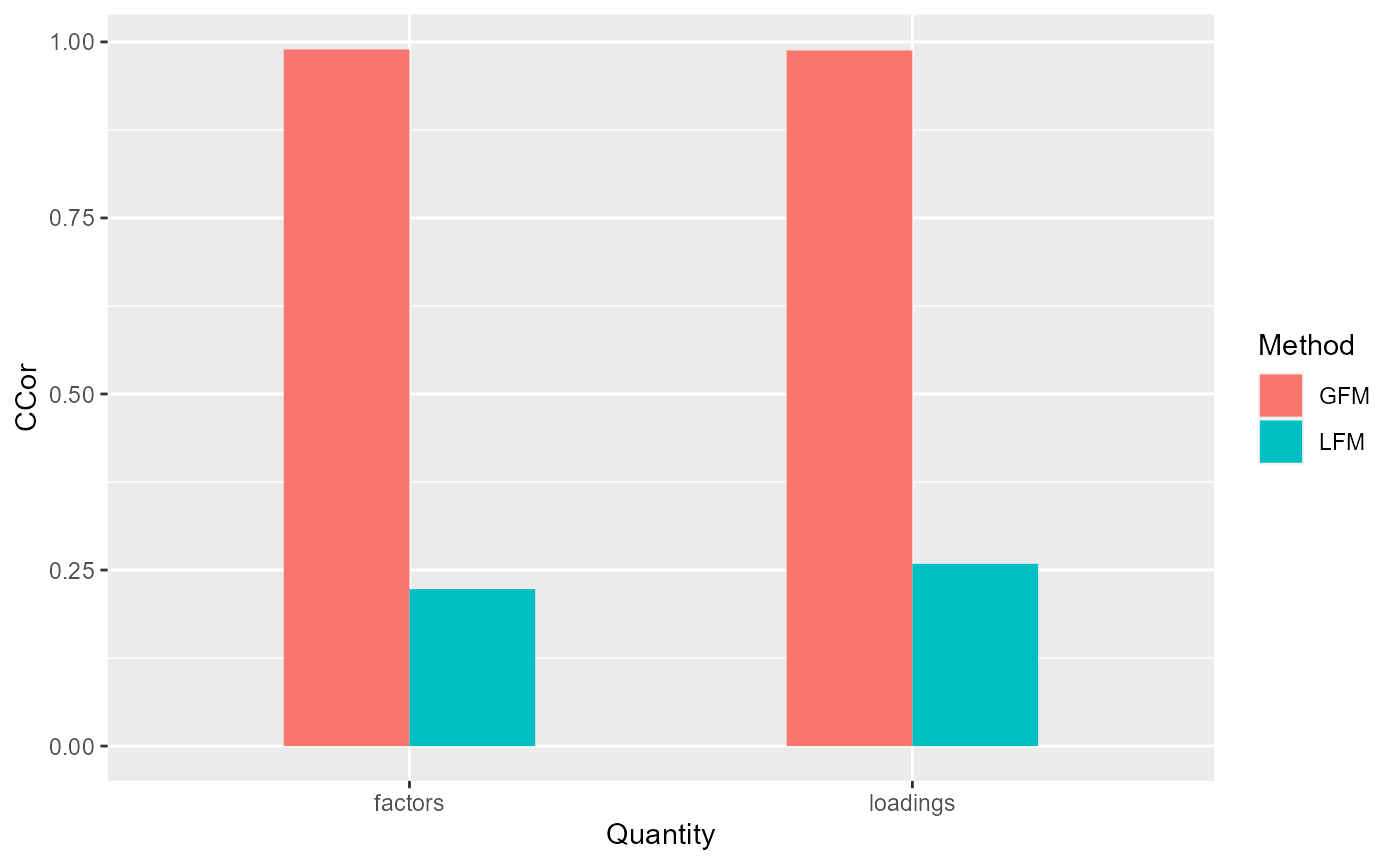

GFM outperforms LFM in analyzing data with the mixed-types of count and categorical variables

First, we generate the data with Count(Poisson) variables and set the parameters of algorithm. Then fit the GFM model with user-specified number of factors.

  dat <- gendata(seed=1, n=200, p=200, type='pois_bino', q=2, rho=2)
  # Obtain the observed data
  XList <- dat$XList # this is the data in the form of matrix list.
  str(XList)
#> List of 2
#>  $ : int [1:200, 1:100] 2 0 3 5 1 1 1 5 1 0 ...
#>  $ : int [1:200, 1:100] 1 0 1 1 0 0 1 0 0 0 ...
  X <- dat$X # this is the data in form of matrix
  # set variables' type, 'gaussian' means there is  continous variable type.
  types <- dat$types
  table(dat$X[,1])
#> 
#>  0  1  2  3  4  5  6  8 11 
#> 52 61 34 26 14  8  3  1  1
  table(dat$X[, 200])
#> 
#>   0   1 
#> 108  92
  # user-specified q=2
  gfm2 <- gfm(XList, types,  algorithm="AM", q=2, verbose = FALSE)
#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred

#> Warning: glm.fit: fitted rates numerically 0 occurred
  measurefun(gfm2$hH, dat$H0, type='ccor')
#> [1] 0.9820777
  measurefun(gfm2$hB, dat$B0, type='ccor')
#> [1] 0.960852

Third, we compare the results with that of linear factor models.

Compare with linear factor models

  lfm1 <- Factorm(dat$X, q=3)
  corH_lfm <- measurefun(lfm1$hH, dat$H0, type='ccor')
  corB_lfm <- measurefun(lfm1$hB, dat$B0, type='ccor')
  
  library(ggplot2)
  df1 <- data.frame(CCor= c(corH_gfm, corH_lfm, corB_gfm, corB_lfm),
                    Method =factor(rep(c('GFM', "LFM"), times=2)),
                    Quantity= factor(c(rep('factors',2), rep("loadings", 2))))
  ggplot(data=df1, aes(x=Quantity, y=CCor, fill=Method)) + geom_bar(position = "dodge", stat="identity",width = 0.5)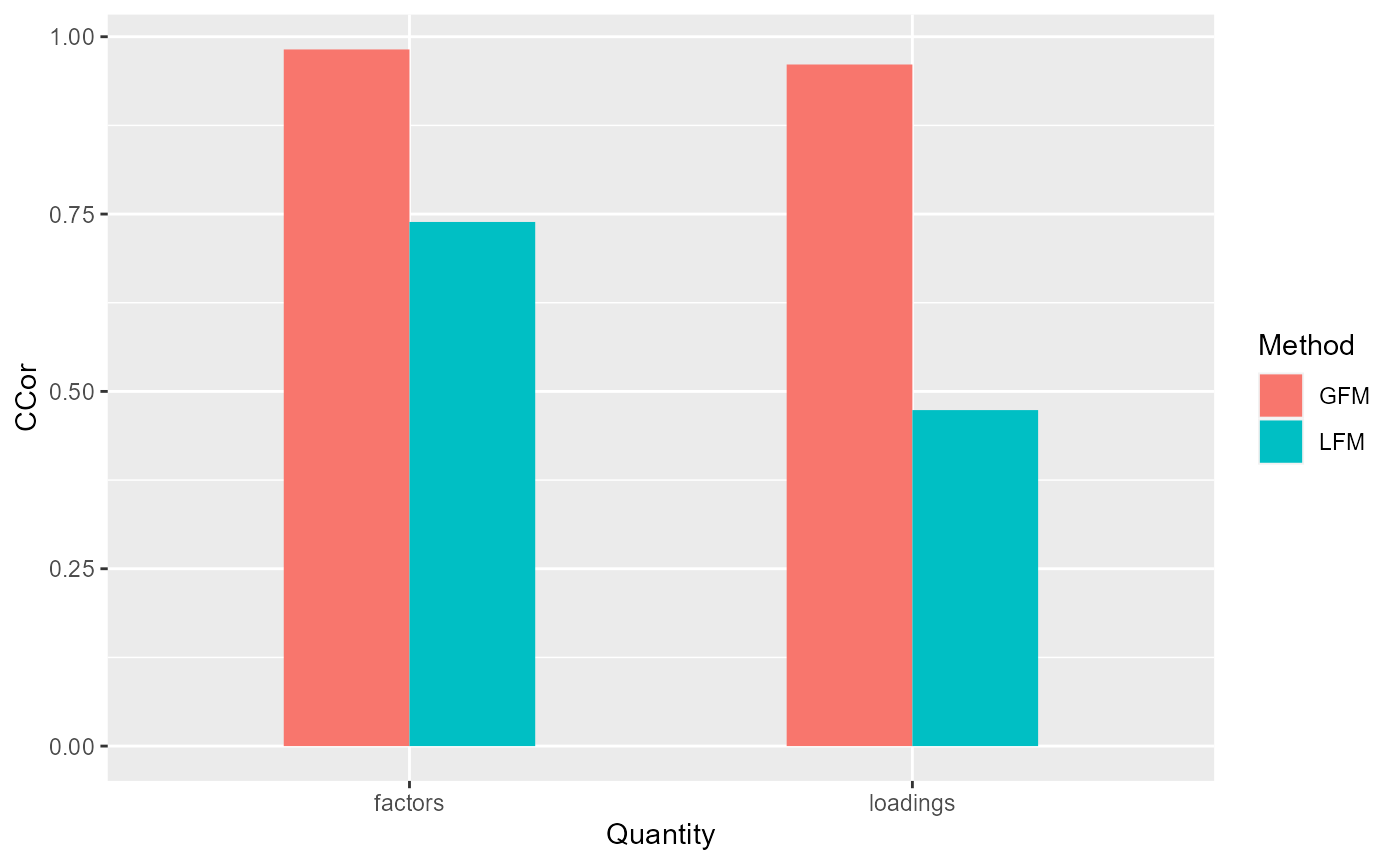

Session information 

sessionInfo()
#> R version 4.1.2 (2021-11-01)
#> Platform: x86_64-w64-mingw32/x64 (64-bit)
#> Running under: Windows 10 x64 (build 22621)
#> 
#> Matrix products: default
#> 
#> locale:
#> [1] LC_COLLATE=Chinese (Simplified)_China.936 
#> [2] LC_CTYPE=Chinese (Simplified)_China.936   
#> [3] LC_MONETARY=Chinese (Simplified)_China.936
#> [4] LC_NUMERIC=C                              
#> [5] LC_TIME=Chinese (Simplified)_China.936    
#> 
#> attached base packages:
#> [1] parallel  stats     graphics  grDevices utils     datasets  methods  
#> [8] base     
#> 
#> other attached packages:
#> [1] ggplot2_3.4.1    GFM_1.2.1        doSNOW_1.0.20    snow_0.4-4      
#> [5] iterators_1.0.14 foreach_1.5.2   
#> 
#> loaded via a namespace (and not attached):
#>  [1] tidyselect_1.1.2  xfun_0.29         bslib_0.3.1       purrr_0.3.4      
#>  [5] lattice_0.20-45   generics_0.1.2    colorspace_2.1-0  vctrs_0.6.1      
#>  [9] htmltools_0.5.2   yaml_2.3.6        utf8_1.2.3        rlang_1.1.0      
#> [13] pkgdown_2.0.6     jquerylib_0.1.4   pillar_1.9.0      withr_2.5.0      
#> [17] DBI_1.1.2         glue_1.6.2        lifecycle_1.0.3   stringr_1.4.0    
#> [21] munsell_0.5.0     gtable_0.3.3      ragg_1.2.2        codetools_0.2-18 
#> [25] memoise_2.0.1     evaluate_0.15     labeling_0.4.2    knitr_1.37       
#> [29] fastmap_1.1.0     irlba_2.3.5       fansi_1.0.4       highr_0.9        
#> [33] Rcpp_1.0.10       scales_1.2.1      cachem_1.0.6      desc_1.4.0       
#> [37] jsonlite_1.8.0    farver_2.1.1      systemfonts_1.0.4 fs_1.5.2         
#> [41] textshaping_0.3.6 digest_0.6.29     stringi_1.7.6     dplyr_1.0.9      
#> [45] rprojroot_2.0.3   grid_4.1.2        cli_3.2.0         tools_4.1.2      
#> [49] magrittr_2.0.3    sass_0.4.1        tibble_3.2.1      crayon_1.5.1     
#> [53] pkgconfig_2.0.3   MASS_7.3-55       Matrix_1.4-0      assertthat_0.2.1 
#> [57] rmarkdown_2.11    rstudioapi_0.13   R6_2.5.1          compiler_4.1.2